4361. Solarium for mushrooms (Hard)
Once again,
Mikhail is conducting his experiments. This time, he decided to clone
mushrooms. For that, he prepared n spores, which he will soon
plant in the ground and grow. To ensure that the spores, as they grow and
expand, do not interfere with each other, Mikhail decided to place them only at
points with integer coordinates.
In addition, to
accelerate their growth, he plans to build a large circular lamp that will warm
the developing mushrooms. He also wants to place the center of the lamp at a
point with integer coordinates, and the lamp’s radius should also be an
integer.
But how should
he choose the appropriate radius? Of course, he could build a lamp large enough
to cover the entire mushroom forest, but that would take a lot of extra time —
and Mikhail doesn’t have much time to spare. Therefore, the radius of the lamp
should be as small as possible.
Input. A single
integer is given – the number of spores n (0 ≤ n ≤
3141592649625).
Output. Print the smallest
possible integer radius of a lamp that can cover all n spores.
|
Sample
input |
Sample
output |
|
5 |
1 |
SOLUTION
binary search
Algorithm analysis
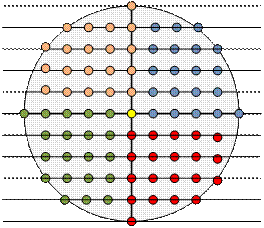
Let us divide the set of
points with integer coordinates into five parts, as shown in the figure: one
point lies at the center, and the remaining four parts are symmetric and cover
the four quadrants of the circle. If the number of points lying in one quadrant
is res, then the total number of points inside the circle will be 4 * res + 1.
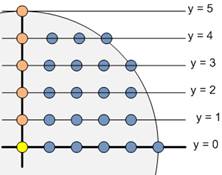
Let’s compute the value of
res. Let the radius of the circle be r. We iterate over the
values of y from 0 to r. Then, on the line y = k (0 ≤ k ≤ r), there will be 
points with integer coordinates
lying inside the circle. The total number of such points across all y
levels gives us the value of res:
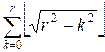
Let f(r) denote the
total number of integer-coordinate points inside a circle of radius r.
Then:
f(r) = 4 * 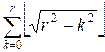+ 1
The function f
is monotonically increasing. The task is to find the smallest value of r
such that the equation f(r) = n holds. We’ll use binary search to
find the required radius r of the lamp.
Algorithm implementation
The function count returns the number of
points with integer coordinates that lie inside a circle of radius r.
long long
count(long long
r)
{
long long res = 0;
double r2 =
r*r;
for(long long y = 0; y
<= r; y++)
res += (long
long)sqrt(r2 - y*y);
return 4 *
res + 1;
}
The main part of the program. Read the input value n.
scanf("%lld",&n);
Search for the radius of the circle that covers at least n points
using binary search. Initially, we assume that the desired radius lies within
the range [l; r] = [0; 1000000].
l = 0; r =
1000000;
while(l < r)
{
m = (l + r ) / 2;
If the number of points inside a circle of radius m is less than n,
increase the left boundary of the interval to m + 1, the radius m is
not sufficient to cover n points. Otherwise, decrease the right
boundary.
if (count
(m) < n) l = m + 1; else r = m;
}
Print the answer.
printf("%d\n",l);